A level与IB数学中,函数值域该怎么求?
在A-level与IB数学中,函数(function)一直扮演着重要的角色,虽然单拿出来可能只是纯数学(Pure mathematics)部分中的一个章节,但是几乎在所有的数学题中都会有对函数的考察,而这其中又已如何求解函数的值域(range)为难点,那么今天我们就来说说函数值域该怎么求?
首先,最基本的求法就是直接求,可以说这是对于学过以下这些初等函数的同学都能够掌握的方法了.

换元法
解一些复杂值域问题时,常用到换元法,即对结构比较复杂的多项式,若把其中某些部分看成一个整体,用新字母代替(即换元),则能使复杂的问题简单化,明朗化,在减少多项式项数,降低多项式结构复杂程度等方面有独到作用。
那下面我们来看下换元法在实际问题中是怎样应用的

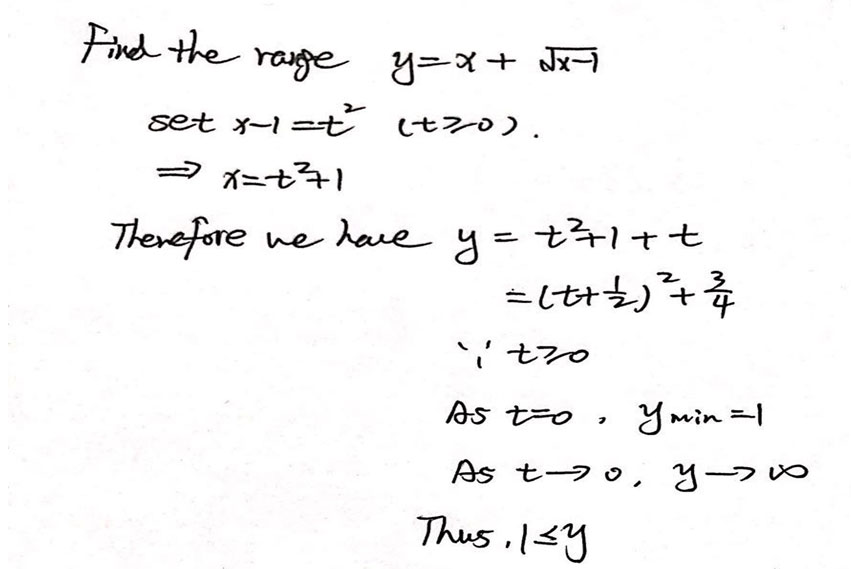
通过这两道经典例题可以看出利用换元法 , 可以化繁为简 , 化难为易 , 从而找到解决函数值域问题的捷径。
判别式法
将原函数变形得到新方程,把此方程看作关于x的一元二次方程,该方程一定有解,利用方程有解的条件求得y的取值范围,即为原函数的值域。
我们同样也看两道例题,如何用判别式法解决考试中的真题。
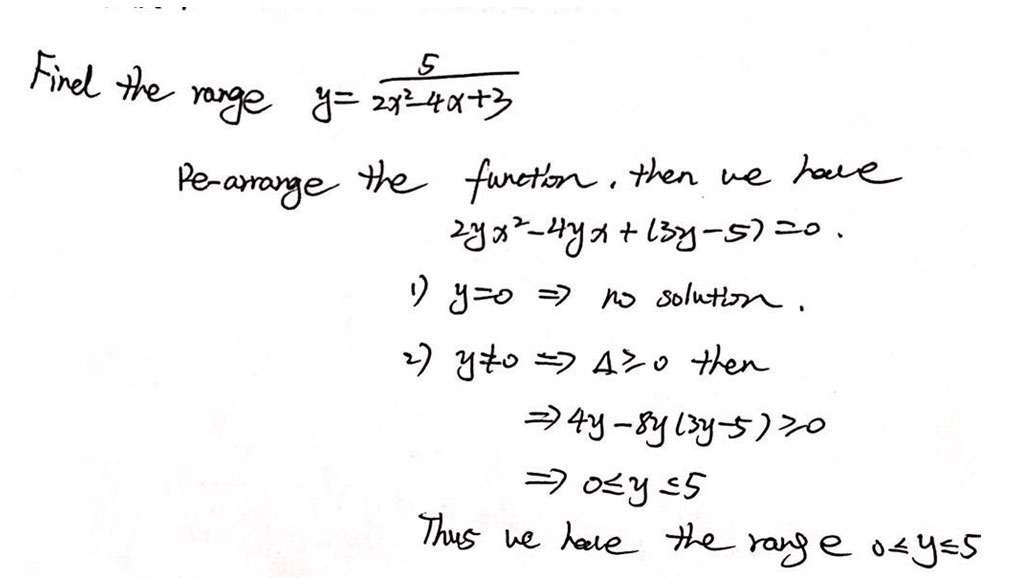

通过这两道题,我相信同学们对于如何运用判别式法求解函数值域已经胸有成竹了。
最后我再总结一下什么时候用换元法,什么时候用判别式法,一般对于一个复杂的函数,里面的多项式我们可以运用换元的手段对其化简,对于形如两个二次多项式比值的函数,我们可以运用判别式法对其求值域。
那么这就是今天全部的内容,如果想了解更多内容,小伙伴们还在等什么,快来A+国际教育中心,A+国际,帮你走向国际!!!
原创:李育霖老师
 喜欢 [0]
喜欢 [0] 相关推荐

- IB考试如何备考才能考出高分?
学习方法 2022-04-24

- IB地理怎么提高?学习中关注这几点!
学习方法 2021-02-25
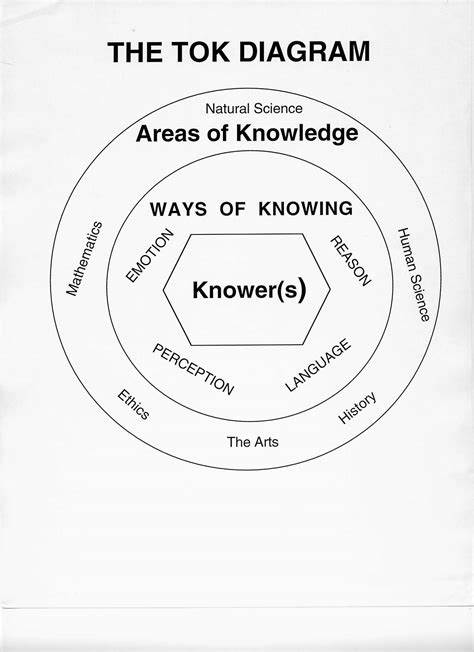
- IB TOK是什么,该如何备考?
学习方法 2021-02-22

- IB经济学课程该怎么学习?
学习方法 2021-02-22