ALevel数学考点正态分布题型解析
尽管很多考试局取消了5月的考试,但也都说明如果对自己的成绩不满意的话,等疫情结束学校开学后还可以参加考试。
而我们都知道只是单纯的指望预估成绩是不靠谱的,有很大风险,所以我们还得和往常一样,继续做好复习工作,以防预估成绩达不到预期。
在ALevel数学 As的备考过程中,建议以知识点为单位进行归类,通过进行区块整理,更容易建立知识点之间的联系,应对综合性的大题。我们就ALevel数学考点正态分布(Normal distribution)这一个知识点,对其中常考题型跟大家分析。

首先我们要明确的一点是正态分布应用的前提是我们在分析连续的数据,比如人的身高,时间等。
在之前学过的histogram中,我们知道area=k*frequency,如果让k为n分之一,那么area=frequency/n,也就是probability,如果我们把数据看作一个整体,我们会得到一个曲线,我们就称这个曲线为概率密度函数(probability density function).
如果我们要想求出一个概率P(a<X<b),那么a与b闭合部分的面积即为所求,也就是x=a,和x=b两条直线之间的部分。
解决这部分概率题我们要会看表,以下为总结的公式可以供大家参考。
For a>0 P(Z<a):查表 P(Z>a)=1-P(Z<a) P(Z>-a)=P(Z<a) P(P<-a)=1-P(Z<a) P(m<Z<n)=P(Z<n)-P(Z<m) P(-a<Z<a)=P(Z<a)-P(Z<-a)=P(Z<a)-(1-P(Z<a))=2P(Z<a)-1 接下来我们看一道真题
↓
The random variable Z~N(0,1) A is the event Z>1.1 B is the event Z>-1.9 C is the event -1.5<Z<1.5 Find a) P(A) b) P(B) c) P(c) d) P(AUC)
解析:首先我们先分析题干一共四道题,所求都是围绕ABC三个概率题,第一个题要求的是大于1.1的概率,根据互补概率公式,我们用1-小于1.1的概率即可。第二道题要求的是大于-1.9的概率,根据概率密度曲线的对称性,我们根据查表求出<1.9的概率即可。第三道题求的是-1.5和1.5中间部分的概率,那么我们直接套公式就行,即P(-a<Z<a)=P(Z<a)-P(Z<-a)=P(Z<a)-(1-P(Z<a))=2P(Z<a)-1。最后一部分是并集,根据概率公式P(AUC)=A事件概率+C事件概率-A和C事件交集的概率可得。
解题步骤如下
↓
P(A)=P(Z>1.1)=1-P(Z<1.1)=1-0.8643=0.1357 P(B)=P(Z>-1.9)=P(Z<1.9)=0.9713 P(C)=P(-1.5<Z<1.5)=2P(Z<1.5)-1=2×0.9332-1=0.8664 A和C的交集=P(1.1<Z<1.5)=P(Z<1.5)-P(Z<1.1)=0.9332-0.8643=0.0698 所以P(AUC)=0.1357+0.8664-0.0698=0.9332
以下为附赠表图
↓
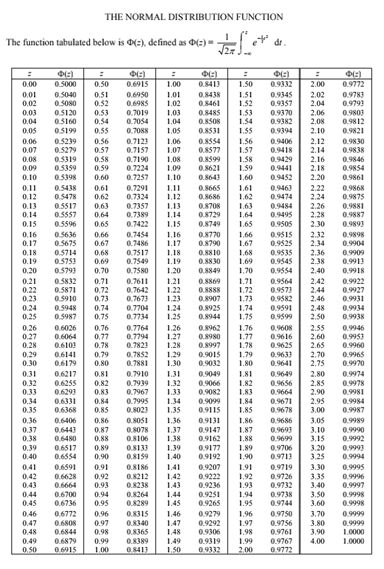
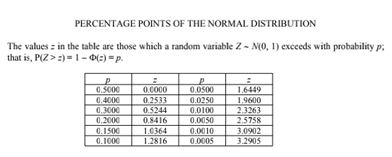
以上就是跟大家分享的正态分布内容,希望对即将入读A-level的学员有所帮助,有疑问欢迎随时联系。
 喜欢 [0]
喜欢 [0] 相关推荐

- 美国‘创世纪计划’:AI技术推动LRAS右移
知识点 2025-11-25

- A-Level物理的逆袭攻略
知识点 2025-11-06

- A-Level物理从C到A*的逆袭攻略
知识点 2025-11-06

- 《A-Level经济:塑造未来经济领袖的基石与卓越辅
知识点 2024-08-14











