a-level数学三角函数知识点学习与介绍
WhatisTrigonometry?
本文为全英叙述,可以充分引领你了解三角函数的前世今生,来龙去脉。在本文结尾处,附上三张三角函数公式表,帮助你自如地应付A-Level数学考试。
Trigonometryisabranchofmathematicsthatstudiesrelationshipsbetweenthesidesandanglesoftriangles.Trigonometryisfoundallthroughoutgeometry,aseverystraight-sidedshapemaybebrokenintoasacollectionoftriangles.
Furtherstill,trigonometryhasastoundinglyintricaterelationshipstootherbranchesofmathematics,inparticularcomplexnumbers,infiniteseries,logarithmsandcalculus.
Thewordtrigonometryisa16th-centuryLatinderivativefromtheGreekwordsfortriangle(trigōnon)andmeasure(metron).ThoughthefieldemergedinGreeceduringthethirdcenturyB.C.,someofthemostimportantcontributions(suchasthesinefunction)camefromIndiainthefifthcenturyA.D.
BecauseearlytrigonometricworksofAncientGreecehavebeenlost,itisnotknownwhetherIndianscholarsdevelopedtrigonometryindependentlyorafterGreekinfluence.AccordingtoVictorKatzin“AHistoryofMathematics3rdEdition)”(Pearson,2008),trigonometrydevelopedprimarilyfromtheneedsofGreekandIndianastronomers.
Anexample:Heightofasailboatmast
Supposeyouneedtoknowtheheightofasailboatmast,butareunabletoclimbittomeasure.Ifthemastisperpendiculartothedeckandtopofthemastisriggedtothedeck,thenthemast,deckandriggingropeformarighttriangle.
Ifweknowhowfartheropeisriggedfromthemast,andtheslantatwhichtheropemeetsthedeck,thenallweneedtodeterminethemast’sheightistrigonometry.
Forthisdemonstration,weneedtoexamineacouplewaysofdescribing“slant.”Firstisslope,whichisaratiothatcompareshowmanyunitsalineincreasesvertically(itsrise)comparedtohowmanyunitsitincreaseshorizontally(itsrun).Slopeisthereforecalculatedasrisedividedbyrun.
Supposewemeasuretheriggingpointas30feet(9.1meters)fromthebaseofthemast(therun).Bymultiplyingtherunbytheslope,wewouldgettherise—themastheight.Unfortunately,wedon’tknowtheslope.Wecan,however,findtheangleoftheriggingrope,anduseittofindtheslope.
Anangleissomeportionofafullcircle,whichisdefinedashaving360degrees.Thisiseasilymeasuredwithaprotractor.Let’ssupposetheanglebetweentheriggingropeandthedeckis71/360ofacircle,or71degrees.
Wewanttheslope,butallwehaveistheangle.Whatweneedisarelationshipthatrelatesthetwo.Thisrelationshipisknownasthe“tangentfunction,”writtenastan(x).Thetangentofananglegivesitsslope.Forourdemo,theequationis:tan(71°)=2.90.(We'llexplainhowwegotthatanswerlater.)
Thismeanstheslopeofourriggingropeis2.90.Sincetheriggingpointis30feetfromthebaseofthemast,themastmustbe2.90×30feet,or87feettall.(Itworksthesameinthemetricsystem:2.90x9.1meters=26.4meters.)
▎Sine,cosineandtangent.
Dependingonwhatisknownaboutvarioussidelengthsandanglesofarighttriangle,therearetwoothertrigonometricfunctionsthatmaybemoreuseful:the“sinefunction”writtenassin(x),andthe“cosinefunction”writtenascos(x).
Beforeweexplainthosefunctions,someadditionalterminologyisneeded.Sidesandanglesthattoucharedescribedasadjacent.Everysidehastwoadjacentangles.Sidesandanglesthatdon’ttoucharedescribedasopposite.Forarighttriangle,thesideoppositetotherightangleiscalledthehypotenuse(fromGreekfor“stretchingunder”).Thetworemainingsidesarecalledlegs.
Usuallyweareinterested(asintheexampleabove)inanangleotherthantherightangle.Whatwecalled“rise”intheaboveexampleistakenaslengthoftheoppositelegtotheangleofinterest;likewise,the“run”istakenasthelengthoftheadjacentleg.Whenappliedtoananglemeasure,thethreetrigonometricfunctionsproducethevariouscombinationsofratiosofsidelengths.
▎Inotherwords:
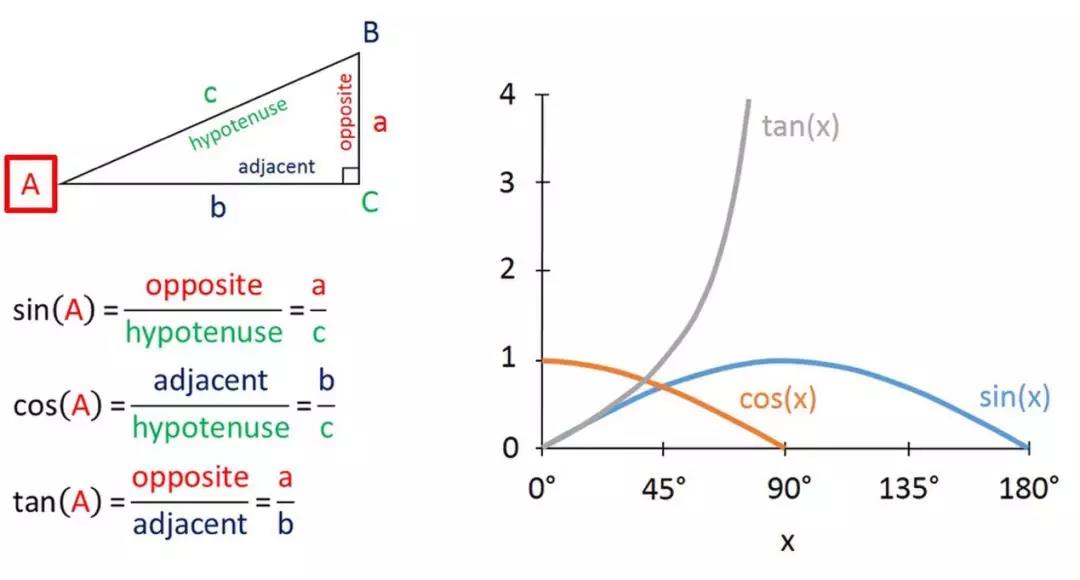
◆ThetangentofangleA=thelengthoftheoppositesidedividedbythelengthoftheadjacentside
◆ThesineofangleA=thelengthoftheoppositesidedividedbythelengthofthehypotenuse
◆ThecosineofangleA=thelengthoftheadjacentsidedividedbythelengthofthehypotenuse
a-level
Fromourship-mastexamplebefore,therelationshipbetweenanangleanditstangentcanbedeterminedfromitsgraph,shownbelow.Thegraphsofsineandcosineareincludedaswell.
▎下为三张三角函数公式表:

a-level数学
 喜欢 [0]
喜欢 [0] 相关推荐

- 美国‘创世纪计划’:AI技术推动LRAS右移
知识点 2025-11-25

- A-Level物理的逆袭攻略
知识点 2025-11-06

- A-Level物理从C到A*的逆袭攻略
知识点 2025-11-06

- 《A-Level经济:塑造未来经济领袖的基石与卓越辅
知识点 2024-08-14










