Alevel数学:考上剑桥的同学都使用的积分技巧
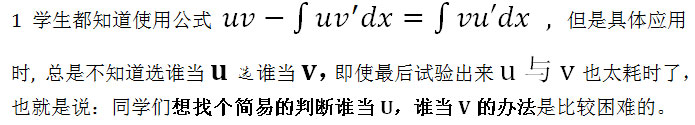
2 学生已经判断出U和V了,但是接下来的积分过程比较慢,想要个快速展开分部积分表达式的方法。
首先我们要想清楚的是:分部积分应用在哪些场景呢? 换句话说,在什么情况下,我们会考虑到使用分部积分?
主要有两个原因:
1被积函数表达式出现了不同类型函数的乘积;
2 在1的基础上,求udv的积分困难,但是求vdu的积分好求时。
基于以上两点,我们的数学系前辈们发明了分部积分。
我们先弄明白了分部积分的诞生来源,接下来需要考虑的是,考试真题或者说平时做题过程中,都会遇到哪些类型的函数进行相乘呢?
A. 如何快速判断出U和V?
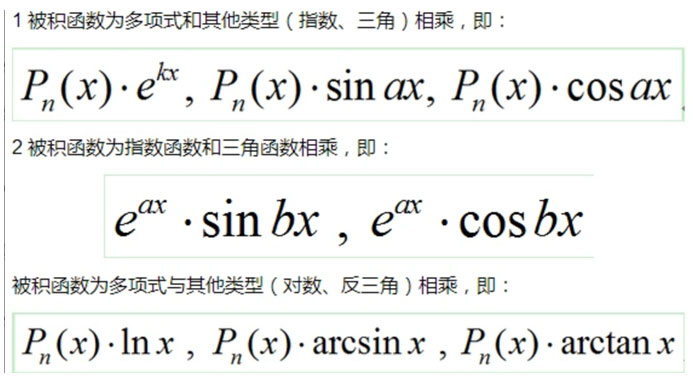
这个U和V就好像是两个人一起干活,一个干求导,一个干积分,现在的目标是积分求出他们两乘积的原函数,你是主人,要协调好这两个人,选出那个易于求导的U和还易于积分的V,让他们干自己容易干的活。诺,你看,现在的情况是出现了dv(对v求导)困难了,而对U求导比较简单(du),因此才出现了分部积分公式。
就拿上面的那3个类型进行说明吧,比如对于第一种类型,多项式和其他类型相乘时,我们选谁当做U呢?当然是选择求导简单的当做U了,而多项式和三角函数、指数函数相乘时,很明显对于多项式更容易求导,因此我们选择多项式做为U。
对于第二种类型,指数函数和三角函数相乘,这两个求导和积分都差不多,选这个当做U或者当做V,都不是什么困难的事,这就是口诀为什么有 “反对幂三指”和“反对幂指三” 两个版本的原因。
对于第三种类型,多项式和对数或者反三角在一块,你这时候就要留意了,因为对于多项式来讲,对它求导或者积分都不是什么困难的事,但是对于反三角函数来说,对它求积分好像确实是有点困难,反倒是对反三角求导比较简单一些。因此,在类型3中,我们往往将对数和反三角函数作为U。
总结一下:当我们碰到一个被积函数为两个不同类型的相乘时,下意识要使用分部积分了,此时你可以不用背口诀,你就简单的想,我让谁去求导且剩下的那个人干积分还不是很困难,那我就选谁当做U。
B.如何快速展开分部积分表达式?

可以看出,这个表格的第一行是写容易求导的人,对U不断地求导,第二行是写容易积分的人,对V不断地做积分,那么,根据表如何写出下来的表达式呢?
口诀就是:“以U为起点,左上右下,错位相乘,正负相间,最后一项写积分”。
有同学会问:我求导到啥时候?正负号如何规定的?用这个表怎么写展开式呢?
对于本题来讲,第一行要对多项式求导至0,。正负号是这样规定的,规定第一项为正,接下来是负号,就这样按顺序写就行。表格的最后一项是积分,被积函数是U的最后一项和V的最后一项的乘积。按顺序写完后,依次写下去整理即可。
再看第二个例子:

由于三角函数在求两次导后,会出现原型,因此,这类一般第一行“求导至循环”。
最后,再来第三个例子:

对于反三角函数或者对数函数做U求导,一般只求一次导,即求导至反三角符号和对数符号消失为止。
通过以上3个例子的介绍,相信大家对这个分部积分的推广公式如何使用应该有了一定的印象
总结一下:对于两个不同的函数乘在一起做积分,我们就要权衡好谁来求导简单一些,谁做积分更容易一些,然后用分部积分的推广公式来展开。
大家可以不用死记硬背分部积分那么长的推广公式,你就记住一点:我对第一行求导,对第二行做相应的积分,求导到什么程度呢?多项式一般是求导到0,三角函数一般是求导至循环,反三角和对数是求导至符号消失,最后利用口诀:“以U为起点,左上右下,错位相乘,正负相间,最后一项写积分”的原则,就可以快速、正确的写出分部积分的表达式!
上述就是今天介绍的主要内容,如果对此内容有疑问,欢迎在线咨询我们的课程顾问老师,A+国际教育中心是国内领先的国际课程辅导机构,专注于为中小龄学员提供国际课程辅导,包括ks1-ks3、GCSE、IGCSE/Pre-A、A-Level、AP、IB等课程学科辅导,同时为申请英美澳加等国家私立初高中的学生提供入学考试辅导,帮助学生顺利入读国外优秀私立学校。目前在北京、英国、美国分别设有授课中心。
 喜欢 [0]
喜欢 [0] 相关推荐

- 进阶数学启航:A加未来Alevel课程 —— 引领未来
学习方法 2024-08-10

- 探索化学世界,A-Level课程引领未来科学精英
学习方法 2024-08-09

- alevel数学课程提升
学习方法 2024-08-06

- "A+未来:A-Level物理考试致胜技巧"
学习方法 2024-08-05









