AP微积分考点解析—幂函数
一般地,y=xα(α为有理数)的函数,即以底数为自变量,幂为因变量,指数为常数的函数称为幂函数。例如函数y=x0、y=x1、y=x2、y=x-1(注:y=x-1=1/x、y=x0时x≠0)等都是幂函数。在AP微积分课程中,关于幂函数的应用也是非常常见的,下面A加未来小编就带大家一起来分析一下这一重要的AP微积分考点,希望对大家有所帮助。
1.Power Functions幂函数y=xμ(μis a constant)
(1)Whenμ=n(where n is a positive integer)
When n is even,the function is also an even function(偶函数);
When n is odd,the function is also an odd function(奇函数);
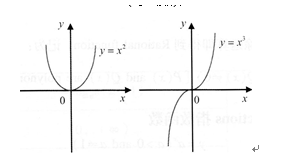
(2)Whenμ=(where n is a positive integer)
When n is even,the domain of the function is(0,+∞);
When n is odd,the domain of the function is(-∞,+∞);
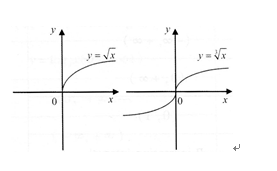
The following figure are the graphs of the functions whenμ=-1,,1,2.
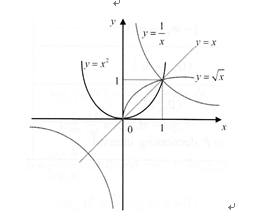
2.Polynomial Functions多项式函数
多个幂函数进行加减乘运算即得到多项式函数,记为:
f(x)=a0xn+a1xn-1+a2xn-2+…+an-1x+an(n is a positive integer or zero)
n=1,linear function(一次函数),f(x)=kx+b(k≠0)
n=2,quadratic function(二次函数),f(x)=ax2+bx+c(a≠0)
n=3,cubic function(三次函数),f(x)=ax3+bx2+cx+d(a≠0)
3.Rational Functions有理函数
二个多项式函数进行除运算即得到Rational function,记为:
f(x)=(Q(x)≠0)[P(x)and Q(x)are polynomial functions]
以上就是A加小编关于AP微积分考点中有关幂函数的一些内容指导,同学们是不是已经很好的掌握了呢?更多AP微积分课程学习问题,欢迎随时咨询我们!
 喜欢 [0]
喜欢 [0] 相关推荐

- 解锁留学双保!1000字指导你留学美国!”
知识点 2024-04-23

- 受疫情影响AP考试取消,出国留学怎么考试?
知识点 2022-06-06

- AP课程解读,考生如何备考?
知识点 2022-06-06

- AP的物理1、物理2和C之间的知识点有什么样的区别
知识点 2021-09-23











