Alevel数学中的弧度制竟有这么大用途？

　　在Alevel数学考试中，有一个章节就是学习弧度制，那么我们先来回忆一下到底什么是弧度呢？

 

 

本章讲师：吴老师

 

　　教师简介：毕业于英属哥伦比亚大学金融专业，4年海外留学及工作经历。研究生毕业后，在加拿大一直从事一线教学工作，主要内容为IB数学、科学的课程讲授，积累了比较丰富的国际教学、教育经验。比较擅长给比较西方化的中国学生授课。目前所授课程为Alevel，IGCSE,IB数学，在理科的教学过程中，喜欢简单、直接，逻辑性强的讲解方式，注重理科思维培养，避免让学生产生惯性思维、以及低效刷题的情况出现。

 

　　弧度等于半径长的圆弧所对的圆心角叫做1弧度的角。

 

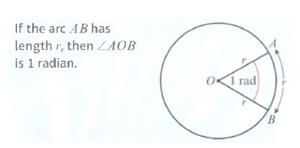
　　如图所示，如果一个圆的半径为r，角度A0B所对应的弧长，与半径相等，那此时的角度定义为1rad。
 

 

　　由于圆弧长短与圆半径之比，不因为圆的大小而改变，所以弧度数也是一个与圆的半径无关的量。同时，通过弧度制，我们可以用角度来表达弧长。
 

 

　　提问时间

 

　　那么为什么要发明弧度制呢？

 

　　在我们了解原因之前，我们先来说一说角度，从我们上小学开始，接触三角形，就会学习角度，会学习如何用量角器测量三角形三个角的角度。

 

　　其实角度的出现，是源于对圆周运动的观察，也就是对太阳的观察。我们的古人，通过对太阳移动轨迹的观察，来计算时间，从而出现了角度。

 

　　然后我们的古人不仅观察太阳，还观察星星，发现了很多星座，发现我们在不同时间看到的星座的位置不一样，然后他们就以星座为参照物，近似观察出这个星座从一开始回到最初位置的周期是360天，也就是一年。

 

　　但随着科学技术的发展，后来古人们又发现，实际上一年是365天，但因为360度已经成为习惯，并且好计算，所以保留了下来。

 

　　古人就是从观察者的角色中，我们认识了角度。其实这个观察者就是看着太阳或者星星做圆周运动。但是如果我们是进行者，我们做圆周运动，要如何计量呢？

 

　　比如我们在航海的时候，就是在做圆周运动，所以“海里”这个为单位也是弧度制的产物之一。

 

　　海里：等于地球椭圆子午线上纬度1分所对应的弧长。如图所示：

 

　　这样，我们知道了航海位移的角度，也就知道我们所处的经纬度，就可以运动地图进行导航。

 

　　同时，如果我们在航海中，用公里运算的话，会产生消暑，这时就非常不容易确定经纬度的定位，是非常不方便的，但是一度是60海里的话，绕赤道一圈就是21600海里，这样计算起来，可以更加精准的在海上定位。

 

　　以上就是A加吴老师对于Alevel数学弧度制的介绍了。弧度制的精髓就在于统一了度量弧与角的单位，从而大大简化了有关公式及运算，尤其在高等数学中，其优点就格外明显。现在大家知道为什么弧度制对于我们来说非常重要了吧～