A加吴老师带你搞定Alevel数学微积分
提起Alevel数学考试,大家最痛恨的单元恐怕就是微积分了吧?
到现在很多小伙伴们心里都有一个疑问,那就是微积分究竟有什么用?发明它到底能解决什么问题?难道就是让我们的考试变得更加困难吗?

本章讲师:吴老师
讲师简介:毕业于英属哥伦比亚大学金融专业, 4年海外留学及工作经历。研究生毕业后,在加拿大一直从事一线教学工作,主要内容为IB数学、科学的课程讲授,积累了比较丰富的国际教学、教育经验。比较擅长给比较西方化的中国学生授课。目前所授课程为Alevel,IGCSE, IB数学,在理科的教学过程中,喜欢简单、直接,逻辑性强的讲解方式,注重理科思维培养,避免让学生产生惯性思维、以及低效刷题的情况出现。 》》详细了解
首先让我们回顾一下我们考试中最常考的题型~求面积!
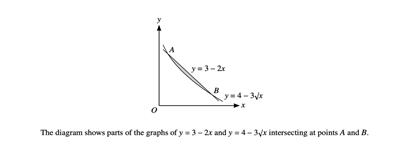
就像上面这道题一样,每次考试我们都会遇到求阴影面积。
从小学开始我们就学习了求各种面积的公式,然后直到现在,随手在纸上画一两条曲线,围成的图形,也来问我们阴影面积,然后那个阴影面积就成了我们心里的阴影。
然而,数学家们不服啊~他们就是想知道有没有万能的方法可以解决这个问题。从古至今,我们解决数学问题的方法,向来就是用我们熟悉的知识去解决未知的领域。
然后数学家们(比如:阿基米德)发现,他们可以把曲线围成的面积,分割成无数个梯形或者矩形之和来无限逼近实际的面积。
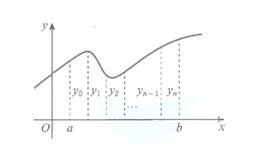
每一个小的梯形拼凑而成
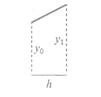
这就是我们学习当中的trapezium rule
但是无论你如何逼近,它都对于数学世界来说,都是有失精准性的,都是粗略的计算,大概的数值。这是骄傲的数学家们无法接受的!
然而,破解这种求曲线面积的关键,竟然藏在一个看起来跟它毫无关联的东西身上,这个东西就是微积分名字里的另一半:
微分(differentiation)
当牛顿和莱布尼茨意识到积分(integration)和微分(differentiation)之间的内在关系之后,数学就迎来了一次空前的大发展。而这神秘的关系就是:
求面积(integration)
&
求导数(differentiation)
竟然是一对互逆的运算。
这也是微积分最核心的思想。然后,人类就可以把微积分的技术扩展到各种其它的领域了,比如求曲线的长度,求曲线的切线,求不规则图形的面积等。
微积分极大的推动了天文学、力学、物理学、化学、生物学、工程学、经济学等自然科学、社会科学及应用科学各个分支中的发展。其实微积分就是一种运算工具,就像加减乘除一样,同时它也真的就像加减乘除一样重要!
所以无论未来大家要学习哪个专业,都让我们认认真真学好微积分吧!
 喜欢 [0]
喜欢 [0] 相关推荐

- 美国‘创世纪计划’:AI技术推动LRAS右移
知识点 2025-11-25

- A-Level物理的逆袭攻略
知识点 2025-11-06

- A-Level物理从C到A*的逆袭攻略
知识点 2025-11-06

- 《A-Level经济:塑造未来经济领袖的基石与卓越辅
知识点 2024-08-14











