IB数学考点解析——对数函数

    一般地，对数函数是以幂（真数）为自变量，指数为因变量，底数为常量的函数。在IB课程学习中，对数函数作为6类基本初等函数之一，是一个非常重要的IB数学考点。今天A加未来小编就带大家一起来详细了解一下IB数学考点中有关对数函数的相关内容，希望对大家有所帮助。

    一般地，如果a（a大于0，且a不等于1）的b次幂等于N(N>0)，那么数b叫做以a为底N的对数，记作logaN=b,读作以a为底N的对数，其中a叫做对数的底数，N叫做真数。

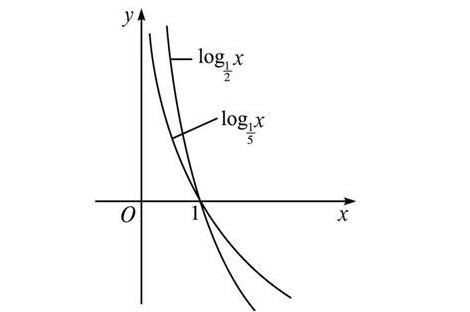
    一般地，函数y=log(a)X，（其中a是常数，a>0且a不等于1）叫做对数函数，它实际上就是指数函数的反函数，可表示为x=a^y。因此指数函数里对于a的规定，同样适用于对数函数。

    对数的性质及定义：

    一.定义：

    若a^n=b(a>0且a≠1)则n=log(a)(b)

    二.基本性质：

    1、a^(log(a)(b))=b

    2、log(a)(a^b)=b

    3、log(a)(MN)=log(a)(M)+log(a)(N)

    4、log(a)(M÷N)=log(a)(M)-log(a)(N)

    5、log(a)(M^n)=nlog(a)(M)

    6、log(a^n)M=1/nlog(a)(M)

    三.对数函数的常用简略表达方式：

    （1）log(a)(b4894/7)=7879log(a989)(b)(a为底数）

    （2）lg(b)=log(10)(b)（10为底数）

    （3）ln(b)=log(e)(b)（e为底数）

    以上就是A加未来小编关于IB数学考点中有关对数函数问题的总结和指导，希望通过本文的介绍，能够帮助同学们更好的理解并掌握对数函数的定义及应用。更多IB课程学习问题，欢迎随时咨询我们！

A加未来国际教育作为国际课程辅导中心（A-level、IGCSE、IB、AP等国际课程），是中国最专业、最值得信赖的国际课程学习中心，是中国学生通往海外顶尖名校的桥梁。详询：010-53666608