GRE数学考试代数与几何常见题型解析

　　代数与几何是数学课程学习中最重要的两大部分，在GRE数学考试中也有着比较多的涉及。今天A加未来小编就带大家一起来解析一下GRE数学考试中几何与代数部分的常见题型以及解题思路，一起来了解一下吧！

01、代数

1、指数运算法则 Rules of Exponents

首先我们要熟练代数的运算法则：

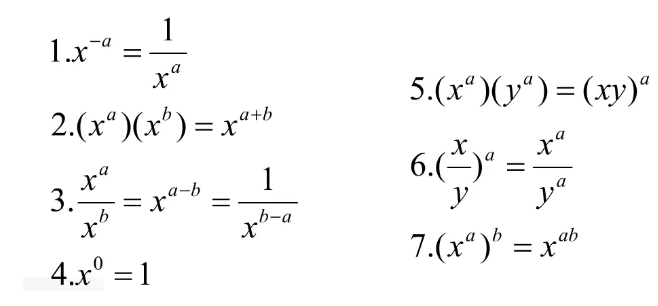
例题一：

Which of the following are equal to （1/560）-4 ?Indicate all correct answers.

通过指数的运算规则可知：

(1/560)^-4=560^4

A:560^4*(560-1)/559=560^4

B:560^-10

C:70^4*8^4=560^4

D:560^8

所以答案为AD

2、函数 Function

y=f（x）称为一个函数

Domain定义域为函数有定义的所有x值

Range值域为函数所有可能的取值

例题二：

★b=b+2 and ub=（b^2+1）/b

QuantityA               Quantity B

u(★3)                   ★(u3)

A.QuantityAis greater.

B.Quantity B is greater.

C.The two quantities are equal.

D.The relationship cannot be determined from the information given.

答案：B

先关注AB的区别，先算括号里，计算顺序不同结果不同

u(★3)=u5=26/5=78/15

★(u3)=★(10/3)=16/3=80/15

u(★3)<★(u3)

3、应用 Applications

3.1、工作问题 work problem

工作量=工作效率ⅹ工作时间

A单独需要a小时完成, B单独需要b小时完成， A和B一起需要c小时完成：

1/a+1/b=1/c

例题三：

Working alone, pump A can empty a pool in 3 hours. Working alone, pump B can

empty the same pool in 2 hours. Working together, how many minutes will it take

pumpAand pump B to empty the pool?

A.72

B.75

C.84

D.96

E.108

答案：A

效率：PA=1/3;PB=1/2

A和B一起工作：1/3+1/2=1/t

那所需要的时间为72分钟

3.2利息问题 interest problem

1、单利

Interest can be computed in two basic ways. With simple annual interest(单利), the interest is computed on the principal only and is equal to (principal)*(interest rate)*time.

 F(本金与利息之和)=P（本金）+P×i（利率）×n（计息期数） =P×(1+i×n)

2、复利

If interest is compounded（复利）, then interest is computed on the principal as well as on any interest already earned.

 F=P*(1+i)^n

例题四：

A certain money market account that had a balance of $48,000 during all of last

month earned $360 in interest for the month.At what simple annual interest rate did

the account earn interest last month?

答案E

月利率：i=360/48000*100%

年利率：I=12i=9%

02、几何

1、三角形性质：

等边三角形 equilateral triangle

直角三角形 right triangle

例题一：

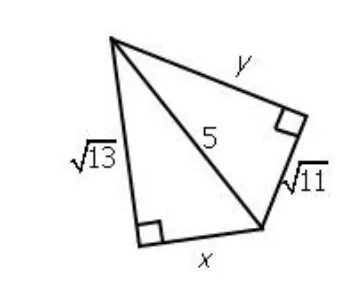
QuantityA       Quantity B

X                     y

A.QuantityAis greater.

B.Quantity B is greater.

C.The two quantities are equal.

D.The relationship cannot be determined from the information given.

答案B

13+x^2=25

11+y^2=25

2、四边形性质

平行四边形 parallelogram

正方形 Square

3、圆 Circles

半径r、圆周率π、直径d、R大半径、h高

圆的面积：πr^2

圆的周长：2πr

半圆的周长：πr+2r

圆环的面积：(R^-r^)π

圆柱的体积：πr^2h

圆柱的表面积：πr^2*2+πdh

圆环的体积：（R^2-r^2）πh

例题二：

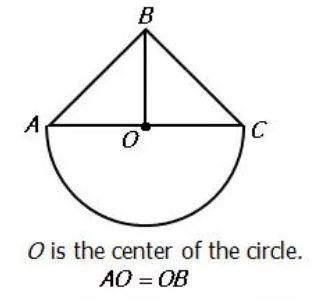
Quantity A                                Quantity    B

Area of semicircular region     Area of triangular region ABC

A.QuantityAis greater.

B.Quantity B is greater.

C.The two quantities are equal.

D.The relationship cannot be determined from the information given.

答案：A

A,B,C都在圆周上，三角形ABC的面积比半圆面积小

4、坐标几何 Coordinate Geometry

1、两点之间距离

设两个点A、B以及坐标分别为

、 ，则A和B两点之间的距离为：

 

2、直线方程

一般式:Ax+By+C=0(A、B不同时为0)【适用于所有直线】

 

，

 

A1/A2=B1/B2≠C1/C2←→两直线平行

A1/A2=B1/B2=C1/C2←→两直线重合

横截距a=-C/A

纵截距b=-C/B

例题三：

In the xy-coordinate system, the distance between points (2√3,−√2)and(5√3,3√2)

is approximately

A.4.1

B.5.9

C.6.4

D.7.7

E.8.1

答案D

用公式：√[(5√3-2√3)^2+(3√2+√2)^2]=√59≈7.7