AP统计学备考四大要点总结
在当今社会发展中,数据统计越来越重要,不少专业领域对于学生统计学知识的掌握也愈发看重,今天A加未来小编就带大家一起来解析一下在AP统计学备考中的一些要点和公式,一起来了解一下吧!

一. Exploring Data
探索性数据分析部分包括分类变量的描述分析和数值型变量的描述分析两部分。
分类变量包含两部分:单变量分类变量部分要了解频数分布表(frequency distribution table),条形图(bar chart)以及饼图(pie chart);双变量分类变量部分要掌握列联表(two-way table)的图形展示方法即对比条形图,如何求列联表中某一个cell对应的expected number
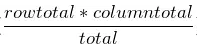 。
。频数分布表 (frequency distribution table),点图(dot plot),条形图(stem plot),直方图(histogram)。
分布的三种形状:对称分布(symmetric distribution)、左偏分布(skew to the left)、右偏分布(skew to the right)
分布中可以体现出的特征:集群和缺口(cluster and gap),异常值(outlier):指与数据中的其他部分有显著不同的数据点。
衡量分布的中心(center of distribution):均值(mean),中位数(median),众数(mode),其中中位数和众数不受outlier的影响。一个mode的数据为unimodal,两个mode的数据为bimodal。
衡量分布的波动(variation of distribution):极差(range)、标准差(standard deviation)以及四分数差(interquartile range)。其中四分位差不受异常值的影响.
衡量分布的位置(position of distribution):四分位数(quartiles)、百分位数(percentiles)以及标准计分(z-score)。
箱线图(boxplot),掌握如何绘制箱线图,并读取箱线图的数据。
对随机变量X进行变换(add or multiple)后,变换后新随机变量的均值,中位数,标准差,四分位数,极差,四分位差等的变换。
散点图(scatterplot),散点图可以反映出:变量之间是否有关系,正关系还是负关系,关系强弱程度。
相关系数(Correlation)是衡量两个变量之间相关程度大小的量,取值范围为[-1,1]。改变变量的计量单位对变量间相关系数的大小没有影响。
最小二乘回归线 (least square regression line),,掌握截距项(intercept)和斜率(slope)两个系数的含义,残差(residual)的定义,判定系数(Coefficient of determination)的含义,残差图(residual plot)及斜率的区间估计和假设检验。
单变量数值型变量 (univariate metric variable) 部分要掌握的主要内容包括:
双变量数值型变量(bivariate metric variable)部分要掌握的主要内容包括:
二. 抽样和实验设计(sampling and experiment)
抽样和实验设计部分需要掌握的主要内容包括:
数据获取的方式主要包括四种:普查、抽样调查、观测研究和实验设计
抽样方法主要包含两种:随机抽样(random sampling)和有偏抽样(biased sampling)。随机抽样主要包括:简单随机抽样(simple random sampling),分层随机抽样(stratified random sampling)、系统抽样(systematic sampling)以及整群抽样(cluster sampling)。有偏抽样主要包括:判断抽样(judgmental sampling)、方便抽样(convenience sampling)以及自愿样本(volunteer sampling)。
抽样中可能存在的误差或偏差。抽样误差(Sampling error)是指由于抽样这一动作所带来的误差,所以不可消除,只能通过一定的手段降低。涵盖不全偏差(undercoverage bias)、无回答偏差(nonresponse bias)以及回答偏差(response bias)等。
实验设计的基本概念
自变量、因变量
混淆变量(confounding):既不是自变量,又不是因变量,但对因变量有影响的变量。
因子(factor):可以简单地当做自变量来理解。水平(Level):因子下的取值个数。处理(Treatment):施加给实验单位的具体处理
控制组(control group),安慰剂(placebo)以及安慰剂组(placebo group)
实验设计的三要素:随机化、控制、实验的可重复性
几种常见的实验设计:
完全随机化设计(completely randomized design)
随机区组设计(randomized block design)
配对设计(matched pairs design)
三. 抽样和实验设计(sampling and experiment)
概率部分要掌握的知识点主要包括:
概率的两个基本准则
互补事件 P(A)+P(A')=1
互斥事件
交集
并集 P(A orB)=P(A)+P(B)-P(A and B)
条件概率 P(A|B)=[P(A and B)]/P(B)
独立的概念 P(A|B)=P(A), P(A and B)=P(A)*P(B)
概率分布部分要掌握的知识点主要包括:
离散型随机变量的概率分布,其中主要涉及均值,标准差的计算。
常见的离散分布:二项分布,如何求概率,以及均值、标准差的计算公式。
常见的离散分布:几何分布,如何求概率。
连续型随机变量的概率分布,掌握对于连续型随机变量的概率分布,概率等于曲线下方所涵盖的面积。
常见的连续型随机变量的概率分布:正态分布(AP统计学中最重要的分布)
如何通过标准化变换得到z-score,
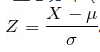 。
。统计量及其抽样分布
这部分需要掌握的主要内容包括:
总体参数以及所对应的样本统计量,如:总体均值对应样本均值,总体方差对应样本方差,总体标准差对应样本标准差,总体比例对应样本比例,总体均值差对应样本均值差,总体比例差对应样本均值差。
样本均值的抽样分布,样本均值如何实现正态分布:
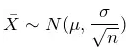
独立样本均值差的抽样分布,样本均值差如何实现正态分布:
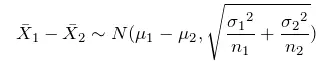
样本比例的抽样分布,样本比例如何实现正态分布:
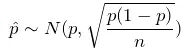
独立样本比例差的抽样分布,样本比例差如何实现正态分布:
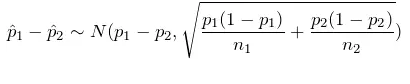
四. 统计推断 (statistical inference)
统计推断包含参数估计和假设检验两部分。
参数估计需要掌握的主要内容包括:
点估计。掌握如何评价一个统计量的好坏。一个好的统计量要具体的特征是:无偏性(unbiasedness)和有效性(efficiency),其中有效是指统计量抽样分布的波动小。
区间估计
区间估计中,首先要掌握置信水平的含义。置信水平95%是指,在多次重复抽样下针对多个样本构建的置信区间中,95%的置信区间包含总体参数值,5%不包含总体参数值。
总体均值 u 的区间估计。掌握总体标准差未知时u的区间估计
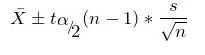
总体比例 p 的区间估计。
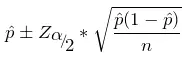
总体比例差
的区间估计。
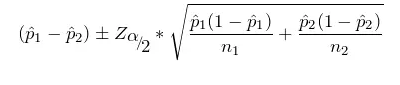
总体均值差
的区间估计。掌握总体标准差未知时
的区间估计:
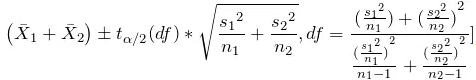 总体均值差
总体均值差 的区间估计(配对样本)。
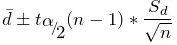
回归直线回归系数
的区间估计。
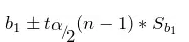
如何确定样本量 n
估计总体均值 u 的情况,利用不等式
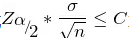 求解。
求解。估计总体均值 p 的情况,利用不等式
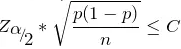 求解。
求解。如何提出零假设
和备择假设
。其中
是搜集样本想要拒绝的假设;而
是搜集样本想要支持的假设。
掌握假设检验的检验统计量。检验统计量就是对应统计量的标准化。
掌握 p-value 的含义。掌握
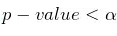 时,拒绝
时,拒绝。
总体均值 u 的假设检验。掌握总体标准差未知时 u 的假设检验,检验统计量为:
总体比例 p 的假设检验。检验统计量为:
总体比例差
的假设检验。检验统计量为:
总体均值差
的假设检验。检验统计量为:
回归直线回归系数
的假设检验。检验统计量为:
单变量分类变量的假设检验(卡方拟合优度检验),检验统计量为:
双变量分类变量的假设检验,卡方独立性检验和比例同质性检验。检验统计量为:
当给定边际误差最大值时,求至少要保证样本量达到多大才会实现对边际误差的控制。
假设检验需要掌握的主要内容包括:
假设检验
以上就是A加未来小编关于AP统计学备考中的要点内容总结,希望能够对大家考试的准备带来一些帮助和参考。更多AP学习问题,欢迎随时咨询我们哟!
 喜欢 [0]
喜欢 [0] 相关推荐

- 解锁留学双保!1000字指导你留学美国!”
知识点 2024-04-23

- 受疫情影响AP考试取消,出国留学怎么考试?
知识点 2022-06-06

- AP课程解读,考生如何备考?
知识点 2022-06-06

- AP的物理1、物理2和C之间的知识点有什么样的区别
知识点 2021-09-23









