AP微积分考试指导：带你了解有关积分方法的常见题型

　　在数学中有一项伟大的发明就是积分，掌握积分的方法可以解决很多理论上的问题进而对实际问题产生重大意义。今天A加未来小编就为大家总结一下在AP微积分考试中有关积分方法的一些内容以及常见题型，希望对大家有所帮助。

　　1.常见公式

　　首先第一波是希望大家一定要牢记的公式

　　每个都必须背起来!

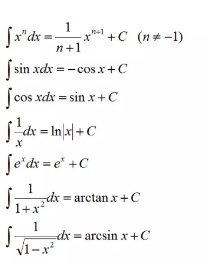
　　第二波公式属于：背不下来，你可以考场上临时推导一下嘛!下一篇推送我们在讲到具体方法的时候在三角函数那一块会来和大家讨论这些式子如何推导。知道推导方法了以后，我们也可以考场上临时求一下。

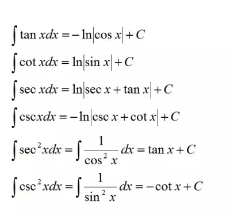
　　2.换元法

　　一般常见的换元法，就不多说了，看到式子不熟悉的情况下，可以尝试用换元来做，但是换元如何选择，选择的好不好也影响到了这道题能不能做出来，方法是否简单。

　　比如下面这个式子：

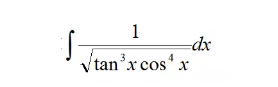
　　如何选择换元呢?你有以下几种选择：

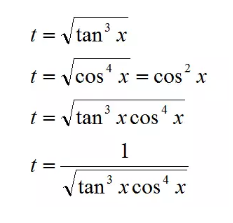
　　怎么选择才是最方便的呢?如何选择换元呢?

　　总不能考试的时候慢慢试探吧。

　　所以希望大家能够熟练的掌握下一种方法：

　　凑微分法!

　　3.凑微分法

　　什么时候使用凑微分的方法?就是当你看到积分式子中有这样的形式可以去凑，并且剩余的部分只和右边括号里面的式子有关系，那么就可以用这样凑微分的方法来计算。

　　比如回到我们刚才的式子：

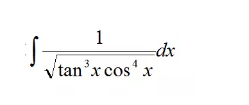
　　如果稍微做出一些变形后，大家可以看到式子可以被变换成：

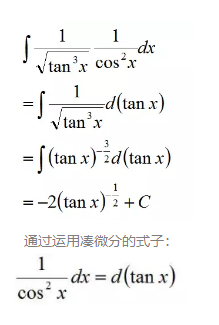
　　可以把一个对x积分的式子变成对tanx积分的式子，同时我们可以观察到，剩下来的部分都是和tanx有关的部分，因此就可以把tanx看成是一个整体来处理。

　　这里如果用换元法去做的话，其实是我们把tanx看成了一个整体进行换元。

　　那么怎么知道这才是正确的换元方法呢?

　　你得对上面的十个式子非常熟悉才可以吧!

　　4.一些特殊形式的规律

　　1.多项式分式

　　如果分母相对来说比较简单

　　(什么叫分母简单呢，就是你把分子全部换成1以后，这样的分式你会积分计算，那就可以判断成分母较为简单)

　　如这样的一些分母：

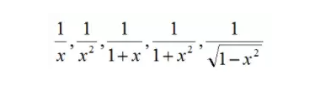
　　这些分母形式都是可以直接套用公式，或者通过简单的换元/凑系数的方法进行快速的积分，因此我们把他们归成简单的分母。

　　(1)如果分子的最高次数大于等于分母的最高次数

　　the highest order of the numerator is greater than or equal to the highest order of the denominator

　　比如这样的：

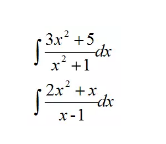
　　分子的最高次数都要大于等于分母的最高次数：

　　我们采取的方法是：拆分子

　　也就是把分子拆成多项来和分母约分，从而让最后的分式只保留分子较为简单的形式：

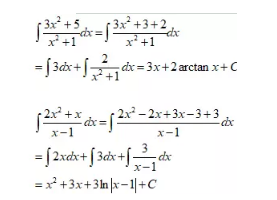
　　(2)如果分母相对来说比较简单，但是分子的次数较小

　　这个时候我们需要对分母进行处理，

　　如果分母出现是二次多项式的形式

　　我们可以把分母根据不同形式分成两种类型

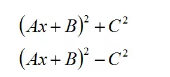
　　如果分母是第一种形式，我们把积分式子往arctan(x)的公式上去凑，比如：

　　如果分母是第二种形式，我们需要进行因式分解，比如：

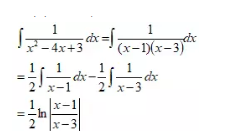
　　不管分子是简单的1，还是关于x的简单的低次多项式，都可以采取这个方法。

　　为了更好的记住多项式分式的做法，

　　大家可以练习下面这个多项式系列↓

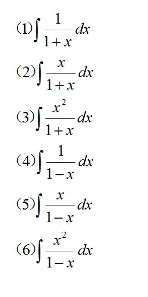
　　我们根据上面讲的方法进行一下归类

　　(1)，(4)，(7)，(13)可以直接用公式适当变形后直接积分。

　　(2)，(3)，(5)，(6)，(9)，(12)，(15)都属于分子最高次数大于等于分母最高次数，因此可以用拆分子的方法计算。

　　(8)，(11),(14)因为分子都出现了xdx，剩余部分都是关于x平方的形式，因此可以用凑微分的方法计算。

　　(10)比较特殊，我们可以把分母因式分解后，拆分成两个分式分别进行计算。

　　以上就是A加未来小编关于AP微积分考试中积分方法内容的介绍，希望通过本文，同学们能够更好的去应对这部分的考试。如果还有什么疑问，欢迎随时咨询我们的线上老师，让专业的AP课程老师一对一为你进行针对性的辅导吧！