奇妙的A-Level数列，你了解透彻了吗？

 

一提起Sequence（数列），大家就马上想起那个被举了无数次，甚至被举烂了的例子，那就是1,2,3,4.

 

在A-Level纯数学的知识结构中，数列（sequence and series）似乎只是一个跑龙套的角色，没什么难度，与核心知识也没什么关联。但我敢保证，它与核心知识（函数和微积分）的关联绝对比你想象的要丰富得多。

 

让我们来回忆一下数列的基础知识
 

数列(sequence/progression)是由若干个数（可能是有限个，也可能有无穷多个）线性排列而成的集合。比如1，3，5，7，9…

 

其中每个数称为数列的项（term），每一项都有它的位置(position)和值(value)。比如，上述数列的第1项（位置）是1（值），第2项是3，第3项是5，……。通常我们un表示第n项的值。因此，对于上述数列，我们可以说u1=1，u2=3，u3=5，……。
 

定义或者表示一个数列通常有三种方式。
 

▎直接列举
 

例1：1，3，5，7，9；

 

例2：u1=1，u2=3，u3=5，u4=7，u5=9。

 

例3：

 

n      (position)	1	2	3	4	5
un    (value)	1	3	5	7	9

 

通项公式general formula
 

如果un可以用n的表达式写出，则这个表达式称为数列的通项公式。利用通项公式，我们就可以根据项的位置，求出项的值。

 

例4：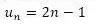 

 

 

递推公式recursive formula/recurrence relation

 

如果数列的相邻项（un和un+1）之间有某种有规律的联系，可以用递推式来定义数列。

 

例5：一个数列用以下两个式子定义，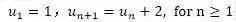

 

不难看出，上述例4-5定义的数列是等价的，并且它们的前5项和例1-3是相同的。

 

▎数列的前n项和(the sum of the first n terms)

 

很多时候，我们不仅关心数列的第n项(the nth term, un)是什么，还关心数列的前n项和(the sum of the first n terms)。

 

前n项和，通常记为Sn，定义为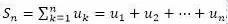

 

 

最常见的两种数列

 

▎等差数列（arithmetic sequence）

 

等差数列理解起来很简单，数列中后一项减去前一项的差值是相等的，这样的一列数就是等差数列。相邻两项的差为常数的数列称为等差数列，这个常数称为公差（common difference）。比如1，3，5，7，9就是个等差数列，它的公差为2。

 

这里还解释了一下算数平均值，arithmetic mean的实际意义。落在两个数中间的那个数，就是算数平均值，实际上，等差数列中连续的三个项，中间的项都是另外的两个项的平均值。

 

我们用a表示等差数列的首项，d表示公差，则有

 

 

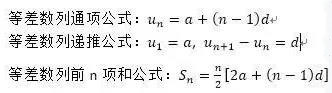
等比数列（geometric sequence）

 

等比数列的定义也是很简单，后一项比上前一项的值是相等的，这个比值叫做公比。相邻两项的比为常数(不能为0)的数列称为等比数列，这个常数称为公比（common ratio）。比如，1，2，4，8，16就是个等比数列，它的公比为2.

 

同样此处也可以介绍几何平均值，geometric mean，理解起来了很简单，就是连续的三个等比（几何）数列中的项，中间的项就是两边的项的几何平均值，中间项的平方等于两边项的乘积。这个知识点一般不会考到，大家知道就行了。

 

我们用a表示等差数列的首项，r表示公差，则有

 

 

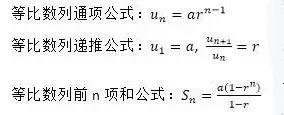
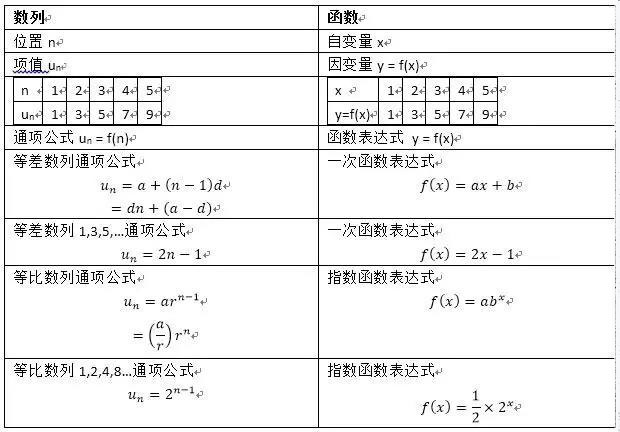
有的同学会问了，你说的这些东西我也知道，可它与函数和微积分能扯上什么关系？关系可大了。我们先关注最明显的关联，只看通项公式。

 

 

我们直接给出结论

 

数列是从自然数集（set of natural number）到任意数集的映射（函数），也就是说，它的实质就是定义域（domain）为自然数的函数。

 

等差数列对应于一次函数(linear function)

 

等比数列对应于指数函数(exponentials)

 

如果你觉得不明显的话，提示一下——我们只需把un写成u(n)，就明白了。如果还不清楚，请把n替换为x，把u替换为f。