igcse数学真题试卷分析,概率题该怎么做?
在历年IGCSE数学考试真题试卷中,都会有一个非常重要的考点在每次考试都会有一道答题,概率这道大题的分数呈现逐年增长的趋势(从6分到8分),那就是Probability(概率)。很多同学在学习IGCSE数学时往往会在概率这个章节徘徊很久,不能很深入的开展学习。不过同学千万不要灰心,今天A+国际教育小编就教大家如何又快又稳地拿到这一部分的分数!

IGCSE数学考试真题试卷概率学问题分析
我们先来看一下IG数学的考试要求,看看大家需要掌握哪些知识点。这可是重点哦!
Probability部分的考纲要求如下:

三个知识点
第一个重要知识点是用树形图求概率。
第二个知识点是用乘法公式求相互独立的事件的概率和用加法公式求互斥事件的概率。
第三个知识点是条件概率的定义和求法。
那么这三个知识点出题人是如何设计的呢?
通常以上三个知识点都会在这一道大题中,用于解决一个现实问题。
让我们一起来看看18年1月份IGCSE数学考试真题试卷中考到的这道概率大题。
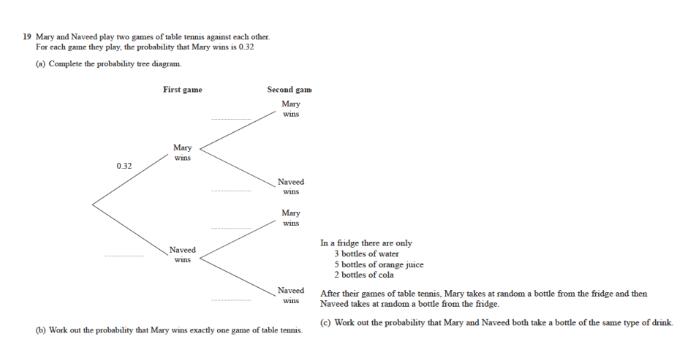
第一问考察的是在树形图(tree diagram)标出概率,每一次游戏结果只能有2种情:Mary wins或者Naveed win,所以他们的概率和为1。需要用到的公式是:

第二问可以从树形图中读出来,Mary只赢一次的情况有2种:第一次Mary赢和第二次Naveed赢或者第一次Naveed赢和第二次Naveed赢。
第一次谁赢和第二次谁赢的概率互不影响,所以这两者为相互独立的事件,我们可以用乘法公式。
Mary只赢一次的2种情况是不可能同时发生的,是互斥的,所以我们可以用加法公式,把这两种情况的概率相加。
第三问考察的是条件概率,在这个情景中,第一个人拿走瓶子后不放回(without replacement),会影响到之后的人拿到不同瓶子的概率。
Marry和Naveed拿到相同瓶子有三种情况:两人都拿到water,两人都拿到orange juice和两人都拿到cola,三种情况之间互斥。
那么这道题的易错点在哪呢?
易错点:需要注意的是第一个人拿走一个瓶子后,后面一个人拿的时候概率会发生改变,这是同学们常常会犯错的地方。比如Mary第一次拿到water的概率是3/10,当Naveed拿饮料时,冰箱里此时只剩下9个瓶子,其中有2瓶water,所以这时候Naveed拿到water的概率是2/9。以此类推,我们可以得到剩下两种情况的概率,把三种情况的概率相加就可以得到正确结果。
最终的答案如下,同学们要注意在做的时候一定要把每一个步骤清晰地写出来哦,步骤也是算分的,所以大家一定要规范答题~
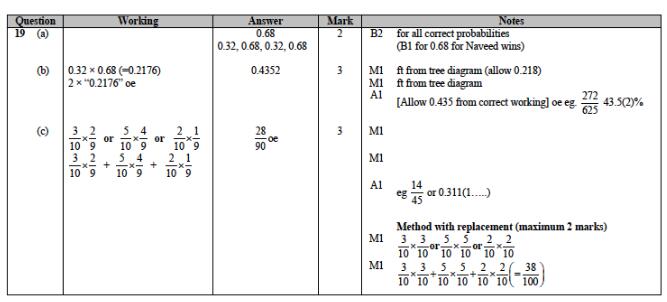
考点总结
总结一下概率大题中经常考察的公式:
P(A)+P(A′)=1,so P(A′)=1−P(A)(P(A)means the probability of event A occurring,P(A′)means the probability of event A not occurring.)
For two independent events(独立事件)A and B,P(A and B)=P(A)P(B)(MULTIPLICATION(‘AND’)RULE)
For mutually exclusive events(互斥事件)A and B,P(A or B)=P(A)+P(B)(ADDITION(‘OR’)RULE)
同学们只要熟练掌握这几个概念和公式,就可以胸有成竹地面对这一道大题啦。怎么样,看完老师的讲解,是不是有种茅塞顿开的感觉。
其实每种题型都有自己的解题方法,只要掌握就可以迎刃而解,化难为易。
 喜欢 [0]
喜欢 [0] 相关推荐

- EPQ不同专业识别揭秘:攻克申请大门的关键!
知识点 2024-04-23

- 解读IGCSE:帮助孩子成功进入名校的关键步骤!
知识点 2024-04-23

- IGCSE在英国大学申请中的重要性
知识点 2024-04-23

- IGCSE商务研究考什么?
知识点 2021-02-18












